Given:
The given triangle is a right angled triangle.
The length of the hypotenuse is 17 units.
One of the legs of the triangle measure x units.
The one of the angles of the right triangle is 60°
We need to determine the value of x.
Value of x:
The value of x can be determined using the trigonometric ratio.
Thus, we have;
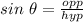
Substituting
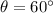 ,
,
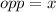 and
and
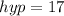 in the above formula, we get;
in the above formula, we get;
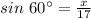
Multiplying both sides of the equation by 17, we get;
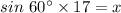
Simplifying, we get;
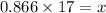
Multiplying, we get;
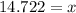
Rounding off to the nearest tenth, we get;
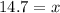
Thus, the value of x is 14.7