Question

9. Water is added to two containers for 16 minutes. The equations below model the ounces of

water, y, in each container after x minutes. At the time after the start when the containers hold
the same amount of water, how much water do they hold?
Container A: y = 16x+104
Container B: y=-2x? +40x+160
36Q ounces
328 ounces
0232 ounces
O 136 ounces

Answer 1

Containers A and B hold the same amount of water, 328 ounces. Hence, if you are on the same connexus assignment, your answer should be option B.

Hope this helps! ;D

Answer 2

The two containers hold 328 ounces at the they hold same amount of water.

Explanation:

The equations below model the ounces of water, y, in each container after x minutes.

`y = 16x + 104`

`y = -2x^(2) +40x+160`

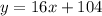
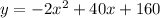
At the time after the start when the containers hold the same amount of water, the two equations must be equal.

⇒
`16 x + 104 = -2x^(2) + 40 x + 160`

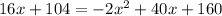
The first step is to divide everything by 2 to make it simplified.

⇒
`8 x + 52 = - x^2 +20 x + 80`

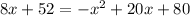
Now put everything on the left .

`x^2 + 8 x - 20 x + 52 - 80 = 0`

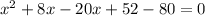
Add the like terms together to further reduce the equation

`x^2 - 12 x - 28 = 0`

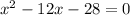
Factorizing the equation to find the roots of the equation.

Here, b = -12 and c = -28

where,

• b is the sum of the roots ⇒ -14 + 2 = -12
• c is the product of the roots ⇒ -14 × 2 = -28

• Therefore, (x-14) (x+2) = 0
• The solution is x = -2 or x = 14

Take x = 14 and substitute in any of the given two equations,

⇒
`y = 16(14) + 104`

⇒
`y =224+104`

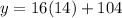
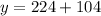
⇒ 328 ounces

∴ The two containers hold 328 ounces at the they hold same amount of water.