Question

1) Find the voltage on a circuit with a resistance of 12.5 Ω if it has a current of 2.35 A.

2) if a circuit with a 9.0 V battery has a current of 6.2 A, how much resistance is in the circuit?

3) A circuit has three resistors with values of 4.0 Ω, 8.0 Ω and 12 Ω. What is the equivalent resistance if they are wired in series?

4) A circuit has three resistors with values of 4.0 Ω, 8.0 Ω and 12 Ω. What is the equivalent resistance if they are wired in parallel?

5) a person with a weight of 956 N runs up a 2.41 m staircase. If it takes 4.17 seconds to reach the top, how much power was generated?

6) a ray of green light was a wavelength of 5.34 x 10^-7 m. What is the frequency?

Answer 1

1. The voltage on the circuit with a resistance of 12.5 Ω and current of 2.35 A is 29.4 V.

2.The resistance in the circuit is found to be 1.45 Ω.

3. The equivalent resistance of the resistors connected in series is 24 Ω.

4. The equivalent resistance of the resistors connected in parallel is 2.18Ω.

5. The power generated is 552.5 W.

6. The frequency of the green light is 0.56×10¹⁵ Hz.

Step-by-step explanation:

1) This problem can be solved using Ohm's law. Here the resistance (R) of the circuit is given to be 12.5 Ω and the current (I) is stated to be 2.35 A. So the ohm's law states that in a closed circuit, the voltage will be directly proportional to the current flowing in the circuit and the resistance will act as the proportionality constant.

`V = I * R = 2.35*12.5 = 29.4 V`

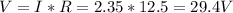
So, the voltage on the circuit with a resistance of 12.5 Ω and current of 2.35 A is 29.4 V.

2) Using the same Ohms' law, now we have to determine the resistance. So in this case, the voltage is given as 9 V and the current is said to be 6.2 A, then resistance can be determined as the ratio of voltage to current.

`R = (V)/(I) =(9)/(6.2) =1.45 Ohms`

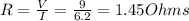
So, the resistance in the circuit is found to be 1.45 Ω.

3) Here, the resistances of three resistors are given as 4 Ω, 8 Ω and 12 Ω. And it is stated that the resistances are connected or wired in series. Then the equivalent resistance will be obtained by the sum of resistances of three resistors, as the current flow will be constant in all the three resistors.

`R_(s) = R_(1) + R_(2) + R_(3) \\ \\R_(s) = 4+8+12 = 24 ohms`

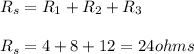
Thus, the equivalent resistance of the resistors connected in series is 24 Ω.

4) Now, if the resistors are connected in parallel, then the equivalent resistance will be ratio of product of resistances to the sum of the resistances.

`(1)/(R_(p) )= (1)/(R_(1) ) + (1)/(R_(2) ) +(1)/(R_(3) )\\\\(1)/(R_(p) )=(1)/(4)+ (1)/(8) +(1)/(12) = (6+3+2)/(24) =(11)/(24) \\\\R_(p) = (24)/(11 ) =2.18 Ohm`

Thus, the equivalent resistance of the resistors connected in parallel is 2.18Ω.

5) Power generated by the person can be obtained by the ratio of work done by the person to the time in which the work is done. So the work done can be obtained by the product of force with displacement.

As here the weight lifted by the person will act as dominant force on the person. So the force is considered as F = 956 N and the displacement is d = 2.41 m, then

`Work done = Force * displacement = 956*2.41 =2303.96 J`

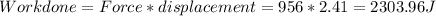
So, the work done is obtained as 2303.96 J and the time is given as 4.17 s, then

`Power = (Work done)/(Time) =(2303.96)/(4.17) =552.5 W`

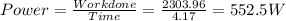
So, the power generated is 552.5 W.

6) In this, the wavelength of green light is given as 5.34 × 10⁻⁷ m. It is known that the wavelength is inversely proportional to the frequency.

`Wavelength = (Speed of light)/(Frequency)`

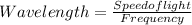
As, speed of light is known as 3×10⁸ m/s, the frequency will be determined as the ratio of speed of light to wavelength.

`Frequency = (Speed of light)/(Wavelength) =(3*10^(8) )/(5.34*10^(-7) ) \\\\Frequency =0.56*10^(15) Hz`

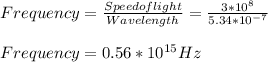
Thus, the frequency of the green light is 0.56×10¹⁵ Hz.