Question

Satellites can be put into elliptical orbits if they need only sometimes to be in high- or low-earth orbit, thus avoiding the need for propulsion and navigation in low-earth

orbits and the expense of launching into high earth-orbit. Suppose a satellite is an elliptical orbit, with a - 4446 miles and b-4420 miles, and with the center of the Earth
being at the origin of the elipse.
a) Write an equation of the orbit of the satellite. Assume that the center of the ellipse is at the origin.
b) The earth has a radius of about 3960 miles. Find the lowest and highest altitudes from the earth to the satellite.

Answer 1

D!

Explanation:

Edge 2022

Answer 2

a)
`(x^2)/(4446^2)+(y^2)/(4420^2)=1`

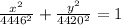
b) Highest Altitude = 486 miles

Lowest Altitude = 460 miles

Explanation:

a)

The standard form of equation of ellipse is:

`(x^2)/(a^2)+(y^2)/(b^2)=1`

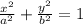
If a > b, then the major axis is horizontal.

If a < b, then the major axis is vertical.

Now, given:

a = 4446

b = 4420

We can write the equation of the ellipse as:

`(x^2)/(a^2)+(y^2)/(b^2)=1\\(x^2)/(4446^2)+(y^2)/(4420^2)=1`

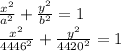
This is the equation, centered at origin.

b)

Since a > b, we can say that the major axis is horizontal and minor axis is vertical.

So, it stretches:

4446 miles from the center of the earth towards both -x and +x axis

and

4420 miles from the center of the earth towards both -y and +y axis

Since, the radius of the earth is 3960 miles, it means from center to earth's surface in all sides is 3960 miles.

The highest and lowest point altitude will be the different in x and y axis (horizontal and vertical) of the point with orbit of the satellite.

4446 - 3960 = 486 miles

and

4420 - 3960 = 460 miles

Thus,

Highest Altitude = 486 miles

Lowest Altitude = 460 miles