Question

Banks sometimes quote interest rates in the form of "add-on interest." In this case, if a 1-year loan is quoted with a 20% interest rate and you borrow $1,000, then you pay back $1,200. But you make these payments in monthly installments of $100 each. What are the true APR and effective annual rate on this loan? Why should you have known that the true rates must be greater than 20% even before doing any calculations? (

Answer 1

Calculate the true APR:

It is given that the compounding period is 12 as the payment is done monthly. The total loan amount is $1,000 with $100 monthly installments at an interest rate of 20%. Annuity is a stream of cash flows that continues for a given number of years. The interest rate is calculated by following method. Use the following formula to calculate the present value:

`Present value of annuity = c[(1)/(r)-(1)/(r(1+r)^(t) )]`

Where,

c —) Monthly payment

r —> Interest rate

t —> Compounding period

Now,

`1000 = 100[(1)/(r)-(1)/(r(1+r)^(12) )]`

We cannot determine the exact value of interest of annuity. Using the trial and error method we can determine the interest rate. We can use the TVM (time value of money) keys in the financial calculator to calculate the value of 'r' as below:

Enter

N = 12

PV = -1000

PMT =100

FV = 0

Now press i and we should find that the monthly rate for this annuity(r) is 2.923% per month.

Effective interest rate is the annualized interest rate using compound interest. Multiply the monthly rate by 12 to obtain APR as below:

APR = Monthly rate x 12

Substitute the values in the formula:

APR = 2.923% x 12

APR = 35.076%

Hence, the APR is 35.076%.

Determine the effective annual rate (EAR):

It is the net annual return received. The monthly rate should be used to calculate the effective annual rate with the help of the formula below:

`1+ effective annual rate = (1 + monthly rate)^(12)`

`1+ effective annual rate = (1 + monthly rate)^(12) -1`

`1+ effective annual rate = (1 + 0.2923)^(12) -1`

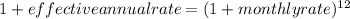
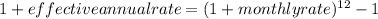
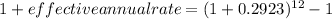
Effective annual rate = 0.41302 or 41.302 %

Hence, the effective annual rate is 41.302%.

Finally we may conclude that the true rate would be 20%, if $1,000 was borrowed today and $1,200 was paid back one year from today. It should be noted that the true rate must be greater than 20% because the twelve annual payment of $100 should be made before the end of the year.