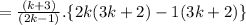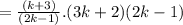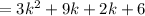Answer:

Explanation:
Factorization of a Quadratic polynomial:
- In order to factorize
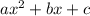 we have to find out the numbers p and q such that, p+q = b and pq=ac.
we have to find out the numbers p and q such that, p+q = b and pq=ac.
- Finding the two integers p and q, we rewrite the middle term of the quadratic as px+qx. Then by grouping of the terms we can get desired factors.
Multiplication of two binomial:
(a+b)(c+d)
=a(c+d)+b(c+d)
=(ac+ad)+(bc+bd)
=ac+ad+bc+bd
Given that,

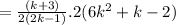 [ taking common 2]
[ taking common 2]
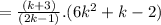 [ cancel 2]
[ cancel 2]