Question

1. David has designed a lawn game that uses a circular center target with alternating gray and

white rings. The circles used to make the target have radii of 0.5 foot, 1 foot, and 1.5 feet.

1.5 ft

What is the total area of the gray sections of the target, to the nearest square inch?

A 452 square inches

B. 565 square inches

C 678 square inches

D. 1017 square inches

Answer 1

Total area of the gray sections of the target is 678 square inches.

Explanation:

Given :

Three concentric circles and we have to find the total area of the gray sections.

Area of white circle having radius 1 foot.

⇒ Area of the white circle - Area of the smaller gray circle.

⇒
`\pi R^2-\pi r^2`

⇒
`\pi (R^2-r^2)`

⇒
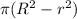
`\pi (12^2-6^2)` ...1 foot = 12 inches and 0.5 foot = 6 inches

⇒
`3.14(144-36)`

⇒
`3.14(108)`

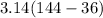
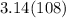
⇒ 339.12 square inches

The total area of the gray sections is the area of the bigger gray circle minus the area of the white circle.

Total area of the gray sections:

⇒
`\pi R^2 - 339.12`

⇒
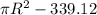
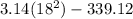`3.14(18^2) -339.12` ....where 1.5 foot = 18 inches

⇒
`1017.36-339.12`

⇒
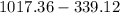
`678.24` square inches.

≅ 678 square inches.

The total area of the gray sections of the target, to the nearest square inch is 678.

Option C is the right choice.