Question

Des Moines’ population in 2005 was about 610 thousand, and had been growing by about 1.2% each year.

a) Write a recursive formula for the population of Des Moines
b) Write an explicit formula for the population of Des Moines
c) If this trend continues, what will Des Moines’ population be in 2017?
d) If this trend continues, when will Des Moines’ population hit 750 thousand?

Answer 1

(a) Recursive formula is
`610 ( 1 + (1.2)/(100))^n`

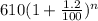
(b) Explicit formula is
`610,000 ( 1 + (1.2)/(100))^1`

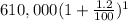
(c) The population in 2017 will be 703876

(d) The population of 750, 000 will reach in 17 years and 4 months

Step-by-step explanation:

Given:

Population in 2005 = 610,000

Rate of increase = 1.2%

(a) Recursive formula = ?

Let n be the number of years:

So, population increase in n years =
`610,000 ( 1 + (1.2)/(100))^n`

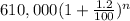
Thus, recursive formula is
`610 ( 1 + (1.2)/(100))^n`

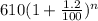
(b) Explicit formula = ?

In one year, the population increase will be
`610,000 ( 1 + (1.2)/(100))^1`

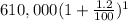
Thus, the explicit formula is
`610,000 ( 1 + (1.2)/(100))^1`

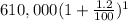
(c)

Number of years between 2005 to 2017 = 12 years

So, population increase in 12 years is
`610,000 ( 1 + (1.2)/(100))^1^2`

P =
`610000 ( 1.154)`

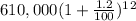
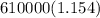
P = 703876

Thus, the population in 2017 will be 703876

(d)

When will the population hit 750,000

Time, t = ?

`750000 = 610000(1+(1.2)/(100))^t\\ \\(75)/(61) = ((101.2)/(100))^t\\ \\1.23 = (1.012)^t\\\\t = 17.4 years`

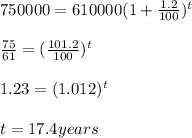
Thus, the population of 750, 000 will reach in 17 years and 4 months