Question

find the x-intercepts and the coordinates of the vertex for the parabola Y equals negative X squared plus 8X -12. If there’s more than one X intercept, separate them commas.

Answer 1

x = 2, and 6

x = 2 , 6

Explanation:

The quadratic function to analyze is:
`y = -x^2+8x-12`

In order to find where the corresponding parabola intercepts the x axis, we set it equal to zero (y = 0):

`y = -x^2+8x-12\\0 = -x^2+8x-12\\x^2-8x+12=0`

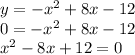
This equation is easy to solve by factoring. We look for a air of integer numbers whose product equals the constant term "12", and whose combinig renders the coefficient of the middle term of the trinomial "-8".

The two such numbers are "-2" and "-6". We use them to split the middle term, and then solve by factoring by grouping:

`x^2-8x+12=0\\x^2-2x-6x+12=0\\(x^2-2x)+(-6x+12)=0\\x(x-2)-6(x-2)=0\\(x-2)(x-6)=0`

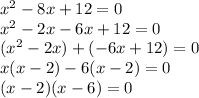
For the product of two factors to render zero, we need either one to be a zero.This means that (x-2)=0 (that is x = 2), or (x-6)=0 (that is x = 6).

So, there are two x-intercepts: x= 2, and 6