Question

A rectangular field is

three times as long as it is wide. If the perimeter of the field is
200 ​yards, what are the​ field's dimensions?(length and width)

Answer 1

The field is 75 yards times 25 yards

L = 75 yards,

W = 25 yards

Explanation:

What we know of the field dimensions is the following:

1) If we name the field width "W", its length is three times that: L = 3 W

2) The field's perimeter is 200 yards. That is the addition of its 4 sides (2 widths and 2 lengths). Then: 2 W + 2 L = 200 yards

SO we basically have two unknowns: "W" and "L", and two linear equations that combine the unknowns, so we can use substitution to replace the length"L" in the second equation by the equivalent expression for the length we got with the first equation (L = 3 W):

`2W+2L=200\\2W+2(3W)=200\\2W+6W=200\\8W=200\\W=(200)/(8) \\W=25 \, yards`

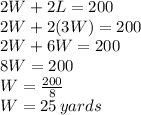
Based on this result, we find the length ofthe field using the substitution equation:

L= 3 W = 3 * 25 yards = 75 yards