A trapezoid has an area of 184 in^2. The height is 8 in and the length of one base is 16 in. Write and solve an equation to find the length of the other base.

Question

asked Jan 20, 2021 64.7k views

1 Answer

Johan Falk · Answer 1 · 2021-01-24T09:45:58+0000

Answer:

The length of other base is 30 in.

Explanation:

Given:

A trapezoid has an area of 184 in^2. The height is 8 in and the length of one base is 16 in.

Now, to get the length of other base.

Let the length of other base be
(b).

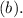
Area of trapezoid
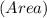(Area) = 184 in².

Height of trapezoid (
) = 8 in.

Length of one base (a) = 16 in.

Now, to get the length of other base of trapezoid we solve an equation:

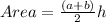
Area=((a+b))/(2) h

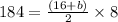
184=((16+b))/(2)* 8

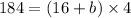
184=(16+b)* 4

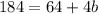
184=64+4b

Subtracting both sides by 64 we get:

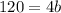
120=4b

Dividing both sides by 4 we get:

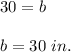
$30=b\\\\b=30\ in.$

Therefore, the length of other base is 30 in.