Answer:
Yes, precipitation of barium iodate will occur.
Step-by-step explanation:
Molarity of barium nitrate solution = 0.050 M
Volume of barium nitrate solution =15.0 mL = 0.0150 L
1 mL = 0.001 L
Moles of barium nitrate = n
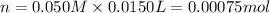
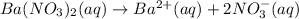
Moles of barium ions:
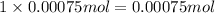
Molarity of potassium iodate solution = 0.10 M
Volume of potassium iodate solution =100.0 mL = 0.1000 L
1 mL = 0.001 L
Moles of potassium iodate = n'
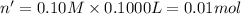
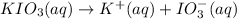
Moles of iodate ions =
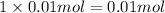
After mixing of both solution in 250 mL in erlenmeyer flask
Volume of the final solution = 250 mL = 0.250 L
Concentration of barium ions in 250 mL solution :
![[Ba^(2+)]=(0.00075 mol)/(0.250 L)=0.003 M](https://img.qammunity.org/2021/formulas/chemistry/college/7lzxn5lg9k2dcd79xe1ris90azbxqwq4tt.png)
Concentration of iodate ions:
![[IO_3^(-)]=(0.01 mol)/(0.250 L)=0.04 M](https://img.qammunity.org/2021/formulas/chemistry/college/p25puf3rvydax2hu6e69p9xvk13u79ttlt.png)
Solubility product of barium iodate,
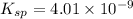
Ionic product of the barium iodate in solution :
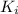
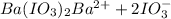
![K_i=[Ba^(2+)][IO_2^(-)]^2](https://img.qammunity.org/2021/formulas/chemistry/college/qtsxkjfb9jdjvm6p3e2g0s20cuwtw1xroh.png)

 ( precipitation)
( precipitation)
As we can see, the ionic product of the barium iodate is greater than the solubility product of the barium iodate precipitation of barium iodiate will occur in 250 mL of final solution.