Question

On a journey of 600 km, a train was delayed 1 hour and 30 min after having covered 1/4 of the way. To arrive on time at the destination, the engine driver had to increase the speed by 15 km/hour. How long did the train travel for?

Answer 1

The train traveled for 32.66 hours.

Explanation:

Let the speed of the train was initially for
`(1)/(4)` the distance was x km/hr.

So, 150 km the train moved with x km/hr speed and the remaining 450 km the train goes with the speed of (x + 15) km/hr.

Then, the time taken by the train to cover the first 150 km will be
`(150)/(x)` hrs.

Therefore, with the actual speed, the train would have covered the 150 km by
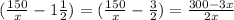`((150)/(x) - 1(1)/(2)) = ((150)/(x) - (3)/(2)) = (300 - 3x)/(2x)` hrs.

Now, from the given conditions, we can write the equation as

`4((300 - 3x)/(2x)) = (150)/(x) + (450)/(x + 15)`

⇒
`2((300 - 3x)/(x)) = 150 * (4x + 15)/(x(x + 15))`

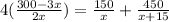
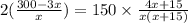
⇒ (300 - 3x) (x + 15) = 75(4x + 15) {Since x ≠0}

⇒ 300x + 4500 - 3x² - 45x = 300x + 1125

⇒ 3x² + 45x - 3375 = 0

⇒ x² + 15x - 1125 = 0

⇒
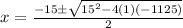`x = \frac{- 15 \pm \sqrt{15^(2) - 4(1)(-1125)}}{2}` {Applying the quadratic formula}

⇒ x = 26.87 km/hr {Ignoring the negative root}

Therefore, the train traveled for
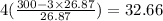`4((300 - 3 * 26.87)/(26.87)) = 32.66` hours. (Answer)