Question

the mass in grams of a radioactive substance is given by M(t) = 700e^-0.002t, where t is in years. what is the half life of the substance

Answer 1

The half life of the substance is approximately 346.6 years

Explanation:

Recall that the half life of a substance is the time it takes for it to decay to half its initial value. That is, based on the formula:

`M(t)=700\,e^(-0.002\,t)`

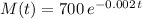
the time it takes for M(t) to reach half of its initial value "700 grams" as per the equation provided. That is 350 grams. So we set the equation that imposes this condition, and solve for the time needed making sure we use logarithms in the process in order to bring the exponents down for the solving:

`M(t)=700\,e^(-0.002\,t)\\350=700\,e^(-0.002\,t)\\(350)/(700) =e^(-0.002\,t)\\ (1)/(2)=e^(-0.002\,t)\\ln((1)/(2))=-0.002\,t\\t=-(ln((1)/(2)) )/(0.002) \\t=346.57\, years`

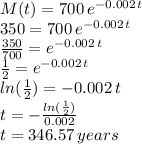
which can be rounded to about 346.6 years