Question

3/20 The winch takes in cable at the rate of 200 mm/s, and this rate is momentarily increasing at 500 mm/s each second. Determine the tensions in the three cables. Neglect the weights of the pulleys.

Answer 1

The tension in the cable
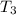`T_3` = 993.5 N

The tension in the cable
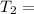`T_2 =` 496.75 N

The tension in the cable
`T_1` = 248.375 N

Step-by-step explanation:

The diagram attached below depicts the full understanding of what the question is all about.

Now, obtaining the length of cable 1 from the diagram; we have:

`L_1 = s_B + 2 s_A ---------- equation \ (1)`

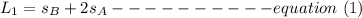
where;

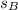`s_B` = distance from the fixed point to point B

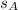`s_A` = distance from the fixed point to pulley A

From the cable 2 as well.we obtain its length

`L_2 = ( s_W - s_A) + s_W ------- equation \ (2)`

where :

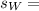`s_W =` distance from the fixed point to the weight attached to the pulley

Let differentiate equation (1) in order to deduce a relation between the velocities of A and B with respect to time ;

Since
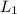`L_1` is constant ; Then:

`(dL_1)/(dt) = (ds)/(dt)+ 2(ds_A)/(dt) ---------- euqation \ (3)`

`0 = v_B +2 v_A`

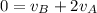
where;

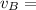`v_B =` velocity at point B

`v_A` = velocity at pulley A

Let differentiate equation (2) as well in order to deduce a relation between the velocities of W and A with respect to time :

Since
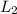`L_2` is constant ; Then:

`L_2 = (s_W - s_A) +s_W`

`(dL_2)/(dt)=2(ds_W)/(dt)-(ds_A)/(dt) ----------- equation \ (4)`

`0 = 2v_W -v_A`

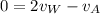
where;

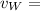`v_W =` the velocity of the weight

Let differentiate equation (3) in order to deduce a relation between accelerations A and B with respect to time

`(dv_A)/(dt) + 2 (dv_A)/(dt ) = 0`

`a_B +2a_A = 0 --------- equation \ (5)`

`a_A = - (1)/(2)a_B`

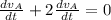
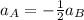
where;

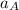`a_A` = acceleration at A

`a_B=` acceleration at B

Replacing 0.5 m/s ² for
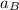`a_B` in equation (5); then

`a_A = - (1)/(2)*0.5`

`a_A = - 0.25 \ m/s^2`

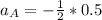
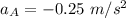
Let differentiate equation (4) in order to deduce a relation between W and A with respect to time

`2(dv__W)/(dt)- (dv_A)/(dt) = 0`

`2a__W} -a_A = 0 ----------- equation \ (6)`

`a__W }= (1)/(2)a_A`

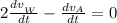
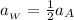
where;

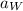`a_W` = acceleration of weight W

Replacing - 0.25 m/s² for
`a_A`

`a__W }= (1)/(2)*(-0.25)`

`a__W }= -0.125 \ m/s^2`

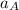
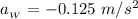
From the second diagram, if we consider the equilibrium of forces acting on the cylinder in y-direction; we have:

`\sum F_y = ma_y`

`mg - T_3 = ma_w`

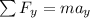
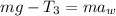
where;

m= mass of the cylinder = 100 kg

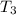`T_3` = tension in the string = ???

g = acceleration due to gravity = 9.81 m/s²

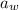`a_w` = acceleration of the cylinder =
`- 0.125 \ m/s^2`

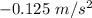
Plugging all values into above equation; we have

(100 × 9.81) -
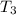`T_3` = 100(-0.125)

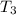`T_3` = 993.5 N

∴ The tension in the cable
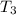`T_3` = 993.5 N

From the third diagram, if we consider the equilibrium of forces acting on the cylinder in y-direction on the pulley ; we have:

`\sum F _y = 0 \\ \\2T_2 -T_3 = 0 \\ \\ T_2 = (T_3)/(2)`

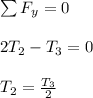
where ;

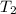`T_2` = tension in cable 2

Replacing 993.5 N for
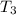`T_3` ; we have

`T_2 = (993.5 \ N)/(2)`

`T_2 = 496.75 \ N`

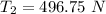
∴ The tension in the cable
`T_2 = 496.75 \ N`

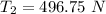
From the fourth diagram, if we consider the equilibrium of forces acting on the cylinder in y-direction on the pulley A ; we have

`\sum F _y = 0 \\ \\2T_1 -T_2 = 0 \\ \\ T_1 = (T_2)/(2)`

where;

`T_1` = tension in cable 1

Replacing 496.75 N for
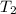`T_2` in the above equation; we have:

`T_1 = (496.75)/(2)`

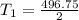
`T_1` = 248.375 N

∴ The tension in the cable
`T_1` = 248.375 N