Question

I’ve never been so confused, this is due in a few minutes, pls help if you can!

Answer 1

Given:

m(ar QT) = 220

m∠P = 54

To find:

The measure of arc RS.

Solution:

PQ and PT are secants intersect outside a circle.

If two secants intersects outside a circle, then the measure of the angle formed is one-half the positive difference of the measures of the intercepted arcs.

`$\Rightarrow \angle P = (1)/(2) (m \ ar (QT) - m \ ar (RS ))`

`$\Rightarrow 54 = (1)/(2) (220- m \ ar (RS ))`

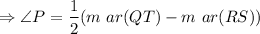
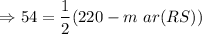
Multiply by 2 on both sides.

`$\Rightarrow 2 * 54 = 2 * (1)/(2) (220- m \ ar (RS ))`

`$\Rightarrow 108= 220- m \ ar (RS )`

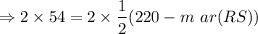
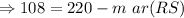
Subtract 220 from both sides.

`$\Rightarrow 108-220= 220- m \ ar (RS )-220`

`$\Rightarrow -112= -m \ ar (RS )`

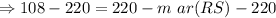
Multiply by (-1) on both sides.

`$\Rightarrow (-112)*(-1)= -m \ ar (RS )*(-1)`

`$\Rightarrow 112= m \ ar (RS )`

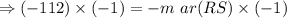
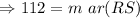
The measure of arc RS is 112.