Question

2NH3(g) CO2(g) In an experiment carried out at this temperature, a certain amount of NH4OCONH2 is placed in an evacuated rigid container and allowed to come to equilibrium. Calculate the total pressure in the container at equilibrium.

Answer 1

The questions involve applying the law of mass action to calculate equilibrium concentrations or partial pressures in chemical reaction scenarios involving gases such as NH3, N2, and H2.

Step-by-step explanation:

The question asks to calculate several equilibrium scenarios in chemical reactions involving gases under different conditions. In these cases, the equilibrium molar concentrations or the changes in partial pressures of gases at equilibrium need to be determined using the principles of chemical equilibrium and the equilibrium constant expressions. The reactions involve ammonia (NH3), nitrogen (N2), hydrogen (H2), and other compounds such as NH4OCONH2, H2O, and CO. To solve these problems, one would apply the law of mass action to establish (Kp or Kc) and use the initial conditions along with the stoichiometry of the reactions to find the equilibrium concentrations or pressures.

Answer 2

The question is incomplete, here is the complete question:

At 25°C, Kp = 2.9 × 10⁻³ for the reaction:

`NH_4OCONH_2(s)\rightleftharpoons 2NH_3(g)+CO_2(g)`

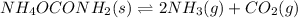
In an experiment carried out at this temperature, a certain amount of NH₄OCONH₂ is placed in an evacuated rigid container and allowed to come to equilibrium. Calculate the total pressure in the container at equilibrium.

Answer: The total pressure in the container at equilibrium is 0.2694 atm

Step-by-step explanation:

Let the initial concentration of
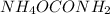`NH_4OCONH_2` be 'x'

The given chemical equation follows:

`NH_4OCONH_2(s)\rightleftharpoons 2NH_3(g)+CO_2(g)`

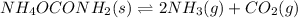
Initial: x

At eqllm: x-y 2y y

The expression of
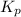`K_p` for above equation follows:

`K_p=(p_(NH_3))^2* p_(CO_2)`

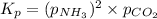
The partial pressure of pure solids and liquids are taken as 1 in equilibrium constant expression. So, the partial pressure of
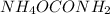`NH_4OCONH_2` is not seen in the expression.

We are given:

`K_p=2.9* 10^(-3)`

Putting values in above expression, we get:

`2.9* 10^(-3)=(2y)^2* y\\\\y=0.0898`

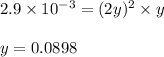
So, the equilibrium partial pressure of ammonia = 2y = (2 × 0.0898) = 0.1796 atm

The equilibrium partial pressure of carbon dioxide = y = 0.0898 atm

Total pressure inside the container at equilibrium =
`p_(NH_3)+p_(CO_2)=[0.1796+0.0898]=0.2694atm`

Hence, the total pressure in the container at equilibrium is 0.2694 atm