Question

5.15 Carbon steel (AISI 1010) shafts of 0.1-m diameter are heat treated in a gas-fired furnace whose gases are at 1200 K and provide a convection coefficient of 100 W/m2 -K. If the shafts enter the furnace at 300 K, how long must they remain in the furnace to achieve a centerline temperature of 800 K?

Answer 1

The shafts must remain in the furnace for approximately 168,517.66 seconds, or 46.78 hours.

How to find time?

Use the lumped heat capacity method and the one-dimensional transient heat conduction equation:

Diameter (d) = 0.1 m

Initial temperature (
`T_i`) = 300 K

Final temperature (
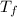`T_f`) = 800 K

Gas temperature (
`T_\infty`) = 1200 K

Convection coefficient (h) = 100 W/m² K

Thermal conductivity of carbon steel (k) ≈ 50 W/m K

Thermal diffusivity of carbon steel (α) ≈ 2.03 x 10⁻⁵ m²/s

Calculate the Biot number:

Bi = h × d / (2 × k)

= (100 W/m² K) × (0.1 m) / (2 × 50 W/m K)

= 0.1

Check if the lumped heat capacity method is valid:

Bi < 0.5, so the lumped heat capacity method can be used. This means can treat the shaft as a single lump of material with uniform temperature throughout.

Apply the transient heat conduction equation:

`(T_f - T_i) / (T_\infty - T_i) = exp(-\alpha t / (d^2 / 4))`

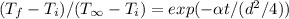
where t = time required to reach the final temperature.

Solve for the time (t):

`t = -(d^2 / 4\alpha) * ln((T_f - T_i) / (T_\infty - T_i))`

`t = - (0.1 m^2 / 4 * 2.03 * 10^(-5) m^2/s) * ln((800 K - 300 K) / (1200 K - 300 K))`

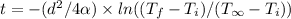
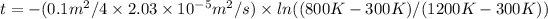
t ≈ 168,517.66 seconds

Therefore, the shafts must remain in the furnace for approximately 168,517.66 seconds, or 46.78 hours.

Answer 2

The time required to reach the center line temperature of 800 K is t = 58 sec

Step-by-step explanation:

Given data

D = 0.1 m

h = 100
`(W)/(m^(2)K )`

Specific heat for carbon steel (C) = 502.4
`(J)/(Kg K)`

Furnace temperature
`T_ o` = 1200 K

Final temperature T = 800 K

Initial temperature
`T_i` = 300 K

From lumped heat analysis

`(T - T_o)/(T_i -T_o) = e^({- (6h)/(\rho C D) } } ) t` ------- (1)

`(6h)/(\rho CD) = ((6)(100))/((7850)(540)(0.1))`

`(6h)/(\rho CD) = 0.001415`

Now from equation (1)

`(800-1200)/(300-1200) = e^(-0.001415t)`

㏑ 0.44 = -(0.001415 ) t

-(0.001415 ) t = - 0.82

t = 58 sec

Thus the time required to reach the center line temperature of 800 K is

t = 58 sec