Answer:
Length of pipe
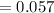 meter
meter
Step-by-step explanation:
Speed of a transverse wave on a string
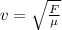
where F is the tension in string and
 is the mass per unit length
is the mass per unit length
Thus,

Substituting the given values we get -

Speed of a transverse wave on a string
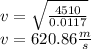
For third harmonic wave , frequency is equal to

Substituting the given values, we get -
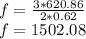
Length of pipe
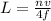
Substituting the given values we get
 for first harmonic wave
for first harmonic wave
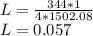
Length of pipe
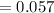 meter
meter