Question

Points A and B are two vertices of an equilateral triangle, what is the perimeter of the triangle? Round to three decimal places.

a) 7.746 units

b) 60 units

c) 20 units

d) 13.416 units

Answer 1

Option c) 20 units is correct

That is the perimeter of the triangle is 20.784 units

Explanation:

Given that the points A and B are two vertices of an equilateral triangle.

To find the perimeter of the triangle

Let a be the side of the triangle

We know that the Area of an equilateral triangle with length of side a is

`Area=(√(3))/(4)a^2` square units

​

Perimeter of the triangle = sum of all sides

=a+a+a

∴ Perimeter of the triangle=3a units

Let equate the Area of the equilateral triangle = Perimeter

Substitute the values we get

`(√(3))/(4)a^2=3a`

`(a^2)/(a)=(3* 4)/(√(3))`

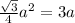
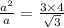
Therefore
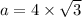`a=4* √(3)` units

Substitute the value of a in the perimeter we get

Perimeter=3a

`3a=3(4* √(3))`

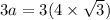
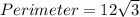`Perimeter=12√(3)` units

=12×1.732

=20.784 units

Perimeter =20.784 units

Hence the perimeter of the triangle is 20.784 units

Option c) 20 units is correct.