Question

Prove algebraically that r = 10/2+2sinTheta is a parabola

Answer 1

`y = - ( 1 )/(10) {x}^(2) + (5)/(2)`

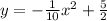
Explanation:

We want to prove algebraically that:

`r = (10)/(2 + 2 \sin \theta)`

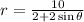
is a parabola.

We use the relations

`{r}^(2) = {x}^(2) + {y}^(2)`

and

`y = r \sin \theta`

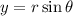
Before we substitute, let us rewrite the equation to get:

`r(2 + 2 \sin \theta) = 10`

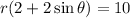
Or

`r(1+ \sin \theta) = 5`

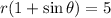
Expand :

`r+ r\sin \theta= 5`

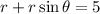
We now substitute to get:

`\sqrt{ {x}^(2) + {y}^(2) } + y = 5`

This means that:

`\sqrt{ {x}^(2) + {y}^(2) }=5 - y`

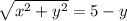
Square:

`{x}^(2) + {y}^(2) =(5 - y)^(2)`

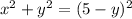
Expand:

`{x}^(2) + {y}^(2) =25 - 10y + {y}^(2)`

`{x}^(2) =25 - 10y`

`{x}^(2) - 25 = - 10y`

`y = - \frac{ {x}^(2) }{10} + (5)/(2)`

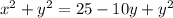
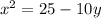
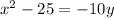
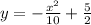
This is a parabola (0,2.5) and turns upside down.