Question

A bank manager has developed a new system to reduce the time customers spend waiting for teller service during peak hours. The manager hopes that the new system will reduce waiting times from the current 9 to 10 minutes to less than 6 minutes.1. Set up the null and alternative hypotheses needed if we wish to attempt to provide evidence supporting the claim that the mean waiting time is shorter than six minutes.2. The mean and the standard deviation of a sample of 100 bank customer waiting times are 5.46 minutes and 2.475 minutes, respectively.

(a) Use the critical value approach to test H0 versus Ha when α = 0.05.

(b) Use the p-value approach to test H0 versus Ha when α = 0.05.

Answer 1

Both the approach gave the same conclusion:

There is enough evidence to support the claim that the mean waiting time is shorter than six minutes

Explanation:

We are given the following in the question:

Population mean, μ = 6 minutes

Sample mean,
`\bar{x}` = 5.46 minutes

Sample size, n = 100

Alpha, α = 0.05

Sample standard deviation, s = 2.475 minutes

First, we design the null and the alternate hypothesis

`H_(0): \mu = 6\text{ minutes}\\H_A: \mu < 6\text{ minutes}`

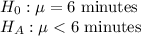
We use one-tailed t test to perform this hypothesis.

Formula:

`t_(stat) = \displaystyle\frac{\bar{x} - \mu}{(\sigma)/(√(n)) }`

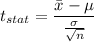
Putting all the values, we have

`t_(stat) = \displaystyle(5.36 - 6)/((2.475)/(√(100)) ) = -2.5858`

a) Use the critical value approach

Now,
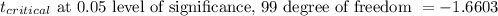`t_(critical) \text{ at 0.05 level of significance, 99 degree of freedom } = -1.6603`Since, the calculated test statistic is less than the critical value of t, we fail to accept the null hypothesis and reject it. We accept the alternate hypothesis.

Conclusion:

Thus, there is enough evidence to support the claim that new system reduces the time customers spend waiting for teller service during peak hours from the current 9 to 10 minutes to less than 6 minutes.

b) Use the p-value approach

The p-value can be calculated as:

P-value = 0.0055

Since the p-value is less than the significance level, we fail to accept the null hypothesis and reject it. We accept the alternate hypothesis.

Conclusion:

Thus, there is enough evidence to support the claim that new system reduces the time customers spend waiting for teller service during peak hours from the current 9 to 10 minutes to less than 6 minutes.