Question

A center for medical services reported that there were 295,000 appeals for hospitalization and other services. For this group, 45% of first-round appeals were successful. Suppose 10 first-round appeals have just been received by a Medicare appeals office. (Round your answers to four decimal places.) (a) Compute the probability that none of the appeals will be successful. (b) Compute the probability that exactly one of the appeals will be successful. (c) What is the probability that at least two of the appeals will be successful

Answer 1

a) 0.0025 = 0.25% probability that none of the appeals will be successful.

b) 0.0207 = 2.07% probability that exactly one of the appeals will be successful.

c) 0.9768 = 97.68% probability that at least two of the appeals will be successful

Explanation:

For each appeal, there are only two possible outcomes. Either it is succesful, or it is not. The probability of an appeal being succesful is independent of other appeals, so we use the binomial probability distribution to solve this question.

Binomial probability distribution

The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

In which
`C_(n,x)` is the number of different combinations of x objects from a set of n elements, given by the following formula.

`C_(n,x) = (n!)/(x!(n-x)!)`

And p is the probability of X happening.

45% of first-round appeals were successful.

This means that
`p = 0.45`

Suppose 10 first-round appeals have just been received by a Medicare appeals office.

This means that
`n = 10`

(a) Compute the probability that none of the appeals will be successful.

This is P(X = 0).

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 0) = C_(10,0).(0.45)^(0).(0.55)^(10) = 0.0025`

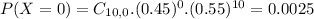
0.0025 = 0.25% probability that none of the appeals will be successful.

(b) Compute the probability that exactly one of the appeals will be successful.

This is P(X = 1).

`P(X = x) = C_(n,x).p^(x).(1-p)^(n-x)`

`P(X = 1) = C_(10,1).(0.45)^(1).(0.55)^(9) = 0.0207`

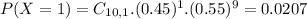
0.0207 = 2.07% probability that exactly one of the appeals will be successful.

(c) What is the probability that at least two of the appeals will be successful

This is
`P(X \geq 2)`

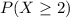
Either less than two appeals are succesful, or at least two are. The sum of the probabilities of these events is decimal 1. So

`P(X < 2) + P(X \geq 2) = 1`

`P(X < 2) = P(X = 0) + P(X = 1) = 0.0025 + 0.0207 = 0.0232`

`P(X \geq 2) = 1 - P(X < 2) = 1 - 0.0232 = 0.9768`

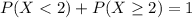
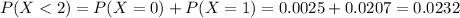
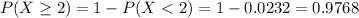
0.9768 = 97.68% probability that at least two of the appeals will be successful