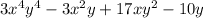Question

Select all the expressions that could represent the volume of a box, which is a fourth degree polynomial in variables x and y.

A. 3x2y2 + 6x2 – 7xy – 14x

B. 10xy + 12x + 2xy2 – y2 – 5y – 6

C. –6 + 7xy + 9x2 + 2x3y

D. 2x3y + 5x2y – xy – 6y

E. 3x4y4 – 3x2y + 17xy2 – 10y

Answer 1

A,C,D

Explanation:

Answer 2

`(E) 3x^4y^4 - 3x^2y + 17xy^2 -10y`

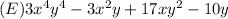
Explanation:

A fourth degree polynomial in variables x and y is a polynomial in which the highest power/index of x and y is 4.

We observe the options below for that which satisfies this condition.

Out of the given options,

`A. 3x^2y^2 + 6x^2 -7xy - 14x\\B. 10xy + 12x + 2xy^2 -y^2 - 5y - 6\\C. -6 + 7xy + 9x^2 + 2x^3y\\D. 2x^3y + 5x^2y - xy -6y\\E. 3x^4y^4 - 3x^2y + 17xy^2 -10y`

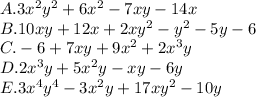
The expression that could represent the volume of a box is

`3x^4y^4 - 3x^2y + 17xy^2 -10y`