Answer
Given,
time = 8 s
θ = 17.5 rad
initial angular velocity = 0 rad/s
Using rotational motion equation
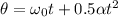
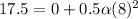
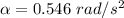
a. angular acceleration

b. Average angular velocity = total angle/total time taken
=
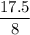 = 2.187 rad/s
= 2.187 rad/s
c. we have,
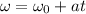
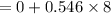
Angular velocity at end of 8 seconds
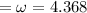 rad/s
rad/s
d. we have, additional angle in next 8 seconds:
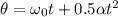
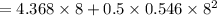
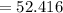 rads
rads