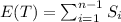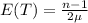Question

A flashlight needs two batteries to be operational. consider such a flashlight along with a set of n functional batteries—battery 1, battery 2, . . . , battery n. initially, battery 1 and 2 are installed. whenever a battery fails, it is immediately replaced by the lowest numbered functional battery that has not yet been put in use. suppose that the lifetimes of the different batteries are independent exponential random variables each having rate μ. at a random time, call it t, a battery will fail and our stockpile will be empty. at that moment exactly one of the batteries—which we call battery x—will not yet have failed.

Answer 1

Question in proper order

A flashlight needs two batteries to be operational. Consider a flash light along with a set of n such batteries-battery 1, battery 2, ..., battery n. Initially, battery 1 and 2 are installed. Whenever a battery fails, it is immediately replaced by the lowest numbered functional battery that has not yet been put into use. Suppose that the life time of different batteries are independent exponential random variables each having a rate A. At a random time, call it T, a battery will fail and our stockpile will be empty. At that moment exactly one of the batteries-which we call battery X-will not yet have failed.

(a). What is P(X = n)?

(b). What is P(X = 1)?

(c). Find E [T].

Answer:

(a) P{ X = n} = 1/2

(b)
`P(X = 1) = ((1)/(2) )^(n-1)`

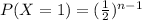
(c)
`E(T) = (n-1)/(\mu)`

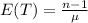
Step-by-step explanation:

The exponential distribution has memoryless property

Due to this property, probability of either battery expire first is 1/2. (Following is the proof of this statement)

Let X and Y(representing two batteries) are independent random variables with exponential distribution, each having rate \mu.

Probability that X fails before Y is given by:-

`P(X<Y) =\int_(x=0)^(\infty)\int_(y=0)^(x) f(x,y)dxdy\\\\=\int_(x=0)^(\infty)\int_(y=0)^(x) \mu e^(-\mu x)\mu e^(-\mu y)dxdy \\ewline \\\\=\int_(x=0)^(\infty) \mu e^(-\mu x)\int_(y=0)^(x)\mu e^(-\mu y)dy dx \\\\=\int_(x=0)^(\infty) \mu e^(-\mu x) (1-e^(-\mu x))dx\\\\ =[-(e^(-\mu x))+((e^(-2\mu x)))/(2)]_(0)^(\infty) \\ewline\\\\`

=
`= 1 - (1)/(2)\\ \\= (1)/(2)`

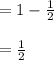
(a) We have to find the probability when the last functional battery is n.

So, P{ X = n} = 1/2

(b)

We have to find the probability when the last functional battery is first battery.

=> 1st battery has life more than 2nd, 3rd, 4th,....nth batteries.

=>1st battery has life more than n-1 batteries.

=>

`P\left \{ X = 1 \right \}=((1)/(2))^(n-1)`

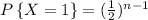
(c)

Random time T can be represented as sum of two random variables representing the lifespan of two batteries used in flashlight.

Let T1 and T2 is lifespan of first two batteries

=> lifespan of flashlight S1 =min(T1 , T2)

As soon as the one the batteries burns out, it will get replaced by another battery.

Using the Memoryless property of exponential distribution, Battery which is not replaced has exponential distribution as if it just started at time of replacement.

Each Si is random variable with rate
`2\mu`,

`E(S_i)= (1)/(2\mu)`

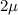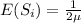
The total lifetime of flashlight

`E(T)=\sum_(i=1)^(n-1)S_i`

`E(T)=(n-1)/(2\mu)`