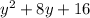Given:
We need to subtract the polynomial
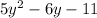 from
from
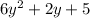
We need to subtract the two polynomials and write the answer in standard form.
Subtraction:
Let us subtract the polynomial
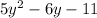 from
from
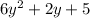
Thus, we have;

Removing the parenthesis, we get;
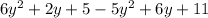
Adding the like terms, we have;
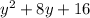
Thus, the value of the two polynomials after subtraction is
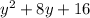
Therefore, the polynomial in standard form after subtraction is