Question

A marching band is arranged in rows of 7 the first row has 3 band members and each row after the first has 2 more band members than the row before it write a rule for the number of band members in the nth row. Then find the total number of band members.

Answer 1

`a_(n)`= 1+2n and 63

Explanation:

the question belongs to arithmetic sequence and
`a_(n)` can be determined by the formula

`a_(n)`= a1 + d (n-1)

Let "
`a_(n)` " represents the number of band members in the nth row

and 'd' represents the common difference.( as stated each row has 2 more band members than the row before it)

therefore, d=2

'a1' represents first row that has three members. So, a1 = 3

->Rule for nth term will be:

`a_(n)`= 3 + 2(n-1)

`a_(n)`= 3 + 2n -2

`a_(n)`= 1+2n

-> In order to find total number of band members '
`S_(7)`'

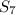Let
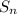`S_(n)` represent total number in n rows

We'll use the formula, i.e
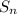`S_(n)` = n/1 (
`a_(1)` +
`a_(n)`)

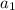where, n is the number of terms,
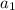`a_(1)` is the first term and
`a_(n)` is the last term

So,

n=7

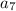`a_(7)` = 1 + 2(7)= 15

=>
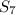`S_(7)` = 7/2 (3 + 15)

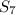`S_(7)` = 63

The total number of band members are 63