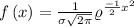Question

Suppose we choose independently 25 numbers at random (uniform density) from the interval [0, 20]. Write the normal densities that approximate the densities of their sum S25

Answer 1

Explanation:

a=0 and b=20 in the uniform density function

∴ the mean μ=
`(1)/(2)\left ( a+b \right )`=
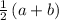`(1)/(2)\left ( 0+20 \right )`=10 and

the variance
`\sigma ^(2)=(1)/(12)\left ( b-a \right )^(2)`=
`(1)/(12)\left ( 20-0 ^(2)\right )`=
`(100)/(3)\\`.

The standard deviation is the square root of the variance, so
`\sigma =\sqrt{(100)/(3)}=(10)/(√(3))`

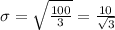
Having determined the mean and standard deviation of the uniform distribution, we can conclude that
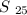`S_(\ 25 )` follows a normal distribution with
`S_(\mu )=n\mu =25\ast 10=250` and
`S_(\\sigma )=\sigma √(n)=(10)/(√(3))\ast √(25)`.

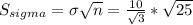The normal probability distribution is:

`f\left ( x \right )=(1)/(\sigma √(2\pi ))\varrho ^{-(1)/(2)}\ast \left ( (x-\mu )/(\sigma ) \right )^(2)`

So, substituting
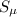`S_(\mu )` and
`S_(\sigma )`

`f\left ( x \right )=(√(3))/(\ 50√(2\pi ))\varrho ^{-(1)/(2)}\ast \left ( (x-250 )/(50√(3)) } \right )^(2)`

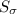
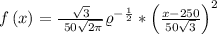
Having approximated sum
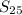`S_(25)`, we move on to the standardized sum
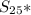`S_(25)\ast`, which is the same
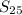`S_(25)` as only with μ=0 and σ=1. This means the probability distribution
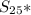`S_(25)\ast` is the standard normal distribution, which is:

`f\left ( x \right )=(1)/(\sigma √(2\pi ))\varrho ^{(-1)/(2)x^(2)}`