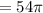Question

A sand storage tank used by the highway department for winter storms is leaking. As the sand leaks out, it forms a conical pile. The radius of the base of the pile increases at the rate of 0.75inches per min. The height of the pile is always twice the radius of the base. Find the rate at which the volume of the pile is increasing when the radius of the base is 6

Answer 1

Rate of change of volume of the pile
`= 54\pi`

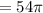
Step-by-step explanation:

Given -

Rate of increase of the base of the pile
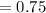`= 0.75` inches per minute

Height of the pile
`= 2 *` the radius of the base

Let "h" be the height of the pile and "r" be the radius of the base.

Then
`h = 2* r`

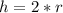
Radius "r"
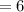`= 6` inches

Rate of change of radius i.e

`(dr)/(dt) = 0.75`

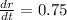
Volume of conical pile

`(\pi )/(3) * r^2 * h\\= (\pi )/(3) * r^2 * 2 * r\\= (\pi )/(3) *2* r^3`

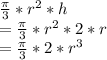
Change in volume of conical pile

`(dV)/(dt) = (dr)/(dt) * (6* \pi * r^2 )/(3)`

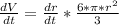
Substituting the value of rate of change of radius, we get -

`(dV)/(dt) = 2 * \pi * (6^2) * (0.75)\\(dV)/(dt) = 54 \pi`

Rate of change of volume of the pile
`= 54\pi`