Question

The Quality Control Department employs five technicians during the day shift. Listed below is the number of times each technician instructed the production foreman to shut down the manufacturing process last week.

Technician Shutdowns

Taylor 5

Hurley 4

Gupta 6

Rousche 5

Huang 4



(a) How many samples, without replacement, of size two are possible?


(b) Compute the mean of the sample means and compare it to the population mean Sample Mean?

Answer 1

(a) There are 10 possible samples of size 2.

(b) The population mean is same as the mean of sample means, 4.8.

Explanation:

The data for the number of times each technician instructed the production foreman to shut down the manufacturing process last week is:

Technician Shutdown

Taylor 5

Hurley 4

Gupta 6

Rousche 5

Huang 4

(a)

Combinations can be used to compute the number of samples of size 2 that are possible from the provided 5 technicians.

`(n!)/(r!(n-r)!)=(5!)/(2!(5-2)!)=10`

Consider the table below for all the 10 possible samples.

(b)

The population mean is:

`\mu=(1)/(n)\sum (Shutdowns)=(1)/(5)* (5+4+6+5+4)=4.8`

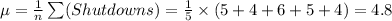
The population mean is 4.8.

Consider the table for the sample means as follows:

The mean of the sample means is:

`\mu_(\bar x)=(1)/(10)\sum (Mean (X_(1), X_(2)))=(4.5+5.5+5+4.5+5+4.5+4+5.5+5+4.5)/(10)=4.8`

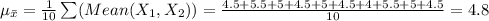
Thus, the population mean is same as the mean of sample means.