Question

A simply supported steel shaft of length L = 37 in is loaded with a uniform distributed load w = 6.5 lbf/in and a point load PA = 350 lbf located at a distance a = 11 in from the left end. Using singularity functions, find the deflections at A and at midspan. Note the percent difference between these two values.

Answer 1

The deflection at A is 1.93×10⁻⁵ in and

The deflection at the midspan is 2.24×10⁻⁵ in

The percentage difference is 15.11 %

Step-by-step explanation:

Here we have

Taking moments about the right end

350 × 26 + 6.5 × 37²/2 = 13549.25 = R₁×37

R₁ = 13549.25 /37 = 366.2 lbf

Weight of steel shaft= 6.5 × 37 = 240.5 lbf

Total downward force = 350 + 240.5 = 590.5 lbf

∴ R₂ = 590.5 lbf - 366.2 lbf = 224.3 lbf

The bending moment equations are

`EI(d^2y)/(dx^2) = M = R_1[x] - 350[x-11]-(wx^2)/(2)`

`EI(d^2y)/(dx^2) = M = 366.2 \cdot [x] - 350[x-11]-(6.5\cdot x^2)/(2)`

By integrating once we have

`EI(dy)/(dx) = 366.2 \cdot ( [x]^2)/(2) - 350\cdot ( [x-11]^2)/(2)-(6.5\cdot x^3)/(6) + C`..................(1)

Second integration gives

`EIy= 366.2 \cdot ( [x]^3)/(6) - 350\cdot ( [x-11]^3)/(6)-(6.5\cdot x^4)/(24) + Cx + B`......................(2)

The boundary conditions are, at x = 0, y = 0 and at x = 37. y = 0

From equation 2 we have at x = 0

`EI(0)= 366.2 \cdot ( [0]^3)/(6) - 350\cdot ( [0-11]^3)/(6)-(6.5\cdot 0^4)/(24) + C0 + B`

Which gives 0 - 0 - 0 + 0 + B Since we ignore the bracket with negative value

When x = 37, equation 2 becomes

`EI(0) = 366.2 \cdot ( [37]^3)/(6) - 350\cdot ( [37-11]^3)/(6)-(6.5\cdot 37^4)/(24) + C\cdot 37 + B`

`EI(0) = 3091521.433- 1025266.67-507585.27 + C\cdot 37`

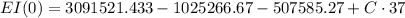
37·C = -1558669.5

C = -42126.2

Therefore we have

`EIy= 366.2 \cdot ( [x]^3)/(6) - 350\cdot ( [x-11]^3)/(6)-(6.5\cdot x^4)/(24) -42126.2\cdot x`

When x = A = 11 in, we have

`EIy= 366.2 \cdot ( [11]^3)/(6) - 350\cdot ( [11-11]^3)/(6)-(6.5\cdot 11^4)/(24) -42126.2\cdot 11`

= -386118.133

y
`_(11)` = -386118.133 /EI = -386118.133 /(200×10⁸ lbf·in²) = -1.93×10⁻⁵ in or 1.93×10⁻⁵ in

At the midspan, we have x = 37/2 in = 18.5

`EIy= 366.2 \cdot ( [18.5]^3)/(6) - 350\cdot ( [18.5-11]^3)/(6)-(6.5\cdot 18.5^4)/(24) -42126.2\cdot 18.5`

EIy = -449228.023 lbf·in⁴

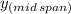`y_((mid \, span))` = -449228.023 lbf·in⁴/(200×10⁸ lbf·in²) = -2.24×10⁻⁵ in or

2.24×10⁻⁵ in

The percentage difference is

`\% \,Difference = (Difference)/((New\,Value+Initial \,Value)/(2) ) * 100 =(2.24-1.93)/((1.93+2.24)/(2) ) * 100` = 0.1511×100 = 15.11 %.