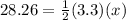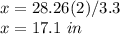Question

A cone and a triangular pyramid have a height of 9.3 m

and their cross-sectional areas are equal at every level
parallel to their respective bases.
What is the height, x, of the triangle base of the
pyramid? Round to the nearest tenth
9.3 in.
6
in.

Answer 1

17.1

Explanation:

Answer 2

`x=17.1\ in`

Explanation:

The complete question is

A cone and a triangular pyramid have a height of 9.3 m and their cross-sectional areas are equal at every level parallel to their respective bases. The radius of the base of the cone is 3 in and the other leg (not x) of the triangle base of the triangular pyramid is 3.3 in

What is the height, x, of the triangle base of the pyramid? Round to the nearest tenth

The picture of the question in the attached figure

we know that

If their cross-sectional areas are equal at every level parallel to their respective bases and the height is the same, then their volumes are equal

Equate the volume of the cone and the volume of the triangular pyramid

`(1)/(3)\pi r^(2)H=(1)/(3)[(1)/(2)(b)(h)H]`

simplify

`\pi r^(2)=(1)/(2)(b)(h)`

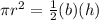
we have

`r=3\ in\\b=3.3\ in\\h=x\ in\\pi=3.14`

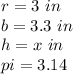
substitute the given values

`(3.14)(3)^(2)=(1)/(2)(3.3)(x)`

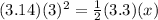
solve for x

`28.26=(1)/(2)(3.3)(x)`

`x=28.26(2)/3.3\\x=17.1\ in`