Answer:
a) electron
b) 0.0758 T
c) 1.0944 A
Question (In proper order)
In the attached figure below, the center of a large bar magnet is z = 25 cm from a thin plate of high-resistance material 12 cm long, 2.5 cm high, and 0.1 cm thick that is connected to a 240 V power supply whose internal resistance is negligible. The bar magnet is perpendicular to the plate. The mobility of charge carriers in the thin plate is 3.8 x 10⁻⁴ (m/s)/(V/m), and the number density of the singly charged charge carriers is 3.6 x 10²³ m⁻³. A voltmeter is connected precisely vertically across the thin plate and reads +1.2 x 10⁻⁵ V. A low-resistance ammeter is in series with the rest of the circuit.
(a) Are the charge carriers electrons or holes?
(b) What is the magnetic dipole moment of the magnet? Include unit. (Enter the magnitude.)
(c) What does the ammeter read, including sign?
Step-by-step explanation:
(a)
The charge carriers in a conductor are electrons and not holes
holes do not move, only electrons are free to move about carrying charges
(c)
we get the ammeter current first before the dipole moment using the formula below
Current I flowing in the plate conductor is given by
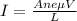
where A = Area of the plate conductor, thickness x B = 0.001m x 0.025m = 0.000025m²
e = charge on the electrons, 1.6 * 10⁻¹⁹C
V = Electric field potential, 240 V
n = density of single charge carriers, 3.6 * 10²³m⁻³
u = mobility of the charge carriers, 3.8 * 10⁻⁴(m/s)/(V/m)
L = Length of the conductor, 1.2 * 10⁻¹m
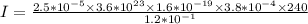
I = 1.0944 A
(b)
From the formula for the hall voltage we get the magnetic dipole moment B which is given by
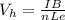
where Vh = hall voltage, 1.2 * 10⁻⁵ V
I = current in the ammeter, 1.0944 A
B = magnetic Dipole moment,
n = number of density, 3.6 * 10²³ m⁻³
L = length of the conductor, 1.2 * 10⁻¹ m
e = charge on the electron. 1.6 * 10⁻¹⁹C
making B the subject in the equation
we have
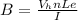

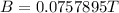
B = 0.0758 T