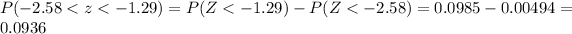Question

According to the latest real estate report from a suburban town, the mean number of home purchases during last quarter was 175 homes with a population standard deviation of 6 homes. A real estate agent believes that the recent increase of mortgage interest rates is causing a decline in home purchases. To test this, the real estate agent randomly selects 60 recent home purchases.

Answer 1

`z_ 1= (173-175)/((6)/(√(60)))= -2.58`

`z_ 2= (174-175)/((6)/(√(60)))= -1.29`

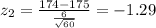
So we want to find this probability:

`P(-2.58<z<-1.29)`

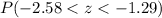
And we can find this probability with this difference:

`P(-2.58<z<-1.29)= P(Z<-1.29)-P(Z<-2.58) = 0.0985 -0.00494= 0.0936`

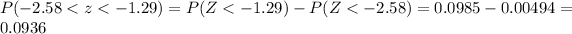
Explanation:

Assuming this complete problem: According to the latest real estate report from a suburban town, the mean number of home purchases during last quarter was 175 homes with a population standard deviation of 6 homes. A real estate agent believes that the recent increase of mortgage interest rates is causing a decline in home purchases. To test this, the real estate agent randomly selects 60 recent home purchases. What is the probability that the mean of this sample of home purchases is between 173 and 174 homes?

Previous concepts

Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".

The Z-score is "a numerical measurement used in statistics of a value's relationship to the mean (average) of a group of values, measured in terms of standard deviations from the mean".

The central limit theorem states that "if we have a population with mean μ and standard deviation σ and take sufficiently large random samples from the population with replacement, then the distribution of the sample means will be approximately normally distributed. This will hold true regardless of whether the source population is normal or skewed, provided the sample size is sufficiently large".

Solution to the problem

Let X the random variable that represent the number of home purchases during the last quarter of a population, and for this case we know the following info

Where
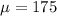`\mu=175` and
`\sigma=6`

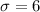
From the central limit theorem we know that the distribution for the sample mean
`\bar X` is given by:

`\bar X \sim N(\mu, (\sigma)/(√(n)))`

And for this case we want to find this probability:

`P(173 < \bar X <174)`

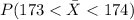
And using the z core formula given by:

`z= (\bar X -\mu)/((\sigma)/(√(n)))`

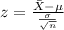
And if we find the z scores we got:

`z_ 1= (173-175)/((6)/(√(60)))= -2.58`

`z_ 2= (174-175)/((6)/(√(60)))= -1.29`

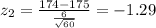
So we want to find this probability:

`P(-2.58<z<-1.29)`

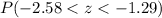
And we can find this probability with this difference:

`P(-2.58<z<-1.29)= P(Z<-1.29)-P(Z<-2.58) = 0.0985 -0.00494= 0.0936`

Answer 2

The probability that the mean of this sample of home purchases is between 173 and 174 is P=0.0936.

Explanation:

The question is incomplete:

"What is the probability that the mean of this sample of home purchases is between 173 and 174?"

To calculate this probability we have to calculate the z-value of 173 and 174, for this distribution (M=175, s.d.=6) and a sample size of n=60.

`z_1=(x_1-\mu)/(\sigma/√(n)) =(173-175)/(6/√(60))= (-2)/(0.775)=-2.58\\\\\\z_2=(x_2-\mu)/(\sigma/√(n)) =(174-175)/(6/√(60))= (-1)/(0.775)=-1.29`

Then, the probability of having a sample mean between 173 and 174 is:

`P(173\leq \bar x \leq174)=P(-2.58<z<-1.29)=P(z<-1.29)-P(z<-2.58)\\\\P(173\leq \bar x \leq174) = 0.09853-0.00494=0.09359`