Question

The equation of a circle is given below.

x^{2}+(y+4)^{2} = 64x

2

+(y+4)

2

=64x, squared, plus, left parenthesis, y, plus, 4, right parenthesis, squared, equals, 64

What is its center?

((left parenthesis

4

,,comma

9

))right parenthesis

What is its radius?

If necessary, round your answer to two decimal places.

Answer 1

Given:

The equation of the circle is
`x^2+(y+4)^2=64`

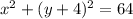
We need to determine the center and radius of the circle.

Center:

The general form of the equation of the circle is
`(x-h)^2+(y-k)^2=r^2`

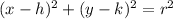
where (h,k) is the center of the circle and r is the radius.

Let us compare the general form of the equation of the circle with the given equation
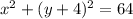`x^2+(y+4)^2=64` to determine the center.

The given equation can be written as,

`(x-0)^2+(y+4)^2=64`

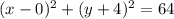
Comparing the two equations, we get;

(h,k) = (0,-4)

Therefore, the center of the circle is (0,-4)

Radius:

Let us compare the general form of the equation of the circle with the given equation
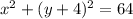`x^2+(y+4)^2=64` to determine the radius.

Hence, the given equation can be written as,

`x^2+(y+4)^2=8^2`

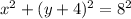
Comparing the two equation, we get;

`r^2=8^2`

`r=8`

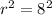
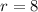
Thus, the radius of the circle is 8