Answer:
The perimeter of the triangle is 24 units.
Explanation:
Given,
Height
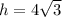
We need to find the perimeter of the equilateral triangle.
Solution,
Firstly we will find out the side length of the triangle.
Since we know that the height of the equilateral triangle is equal to
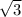 divided by 2 and then multiplied with side of the triangle.
divided by 2 and then multiplied with side of the triangle.
The equation for height of the triangle can be written as;

where 'a' is the side of the triangle.
On substituting the value of 'h', we get;
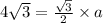
On multiplying both side by
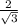 using multiplication property, we get;
using multiplication property, we get;
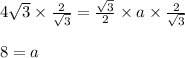
So we get the value of 'a' which is 8.
Here also given that the triangle is equilateral that means the length of all the three sides are equal.
And we know that the perimeter of a triangle is equal to sum of all the three sides.
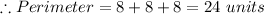
Hence The perimeter of the triangle is 24 units.