Question

The length of a rectangle is 2 centimeters less than its width. What are the dimensions of the rectangle if its area is 195 square centimeters?

Answer 1

Length=15 cm

Width=13 cm

Explanation:

-Let x be the width dimension, the length will be (x-2)

-The area of a rectangle is given by the formula;

`A=lw`

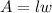
#We substitute the length and width values and equate to the given area:

`A=lw\\195=x* (x-2)\\\\195=x^2-2x`

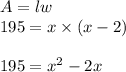
#Rewrite as a quadratic and solve for x:

`195=x^2-2x\\\\x^2-2x-195=0\\\\\# Use \ the \ Quadratic\ formula \ to\ solve:\\\\x_1,x_2=(-b\pm√(b^2-4ac))/(2a)\\\\\therefore x_1,x_2=(-(-2)\pm√((-2)^2-4* 1*(-195)))/(2* 1)\\\\\\x_1=15, x_2=-13`

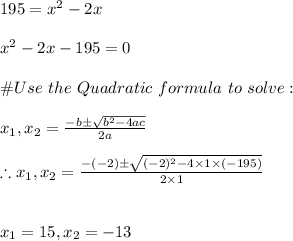
Since dimensions are always positve, the x value is 15

x=15

x=13

Hence, the dimensions of the rectangle are length=15 cm and width=13 cm