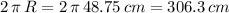Answer:
The length of the arc =
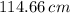
And the length of the full circle:
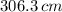
Explanation:
To solve this problem we will be analyzing aright angle triangle that is formed when drawing the appropriate radius associated with the arc and the chord of a segment of circumference as depicted by the triangle shaded in yellow in the attached image.
Notice that the information given in this problem can be represented by:
1) the 90 cm width of the arc with the value of 2x (drawn in orange) in the drawing
2) the 30 cm of the arc's height with the value of y (drawn in green) in the drawing
In order to use the Pythagorean theorem in the little yellow triangle, notice that the hypotenuse is given by the radius R of the circle, and the two legs of the right angle triangle are given by "x" and "R-y"
So the Pythagoras theorem becomes:

Therefore, in our case, where x=45 cm, and y=30 cm, we have:
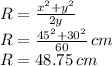
Now, with the radius, we can calculate the length of the arc of circle if we know the subtended angle in radians:
length of arc =
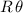
The angle
 subtended by the arc can be obtained by doubling the angle with vertex at the circle's center in our yellow right angle triangle. This is done via the sine function:
subtended by the arc can be obtained by doubling the angle with vertex at the circle's center in our yellow right angle triangle. This is done via the sine function:
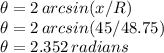
Therefore, length of the arc =
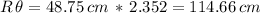
And the length of the full circle: