Question

An isosceles triangle has two congruent sides, and the

angles opposite those sides are congruent. River says that right triangle
ABC cannot be an isosceles triangle. Give a counterexample to show that
his statement is incorrect.​

Answer 1

Answer with Step-by-step explanation:

Isosceles triangle :In this triangle two sides are congruent and the angles opposite those sides are congruent.

Right triangle: In this triangle ,one angle is equal to 90 degree.

Suppose a right triangle ABC in which

Angle A=Angle B,Angle C=90 degree

`\angle A+\angle B+\angle C=180^(\circ)`

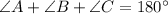
Using triangle angles sum property

Substitute the values

`\angle A+\angle A+90=180`

`2\angle A=180-90=90`

`\angle A=(90)/(2)=45^(\circ)`

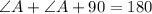
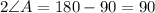
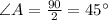
Therefore,

A right triangle in which two equals angle are of 45 degree then the right triangle is an isosceles triangle.

Hence, River's statement is incorrect.