Question

Find the absolute maximum and absolute minimum values of f on the given interval.


`f(x) = 7 + 54x + 2x^(3)` , [0, 4]
absolute minimum value _________
absolute maximum value __________

Answer 1

Absolute minimum value: 7

Absolute maximum value: 351

Explanation:

Absolute Maxima and Minima of Functions

The procedure to find the extreme values of a function in a given interval is:

• Compute the first and second derivatives
• Equate the first derivative to 0 and find the critical points
• Evaluate the critical points in the second derivative to discriminate between maximum and minimum values
• Evaluate the critical points and the endpoints in the original function. The maximum of all the values will be the absolute maximum and the minimum of all the values will be the absolute minimum.

Let the function be

`f(x)=7+54x+2x^3`

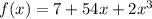
In the interval [0,4]

Compute the first derivative

`f'(x)=54+6x^2`

Equating to 0

`54+6x^2=0`

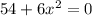
Solving

`x^2=-9`

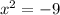
We can find no real solutions to the above equation and therefore there are no critical points. The only possible extreme values will come from the endpoints. Thus

`f(0)=7+54(0)+2(0)^3=7`

`f(4)=7+54(4)+2(4)^3=351`

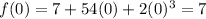
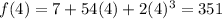
Absolute minimum value: 7

Absolute maximum value: 351