Question

The reading on a voltage meter connected to a test circuit is uniformly distributed over the interval (θ, θ + 1), where θ is the true but unknown voltage of the circuit. Suppose that Y1,Y2,...,Yn denotearandomsampleofsuchreadings. a Show that Y is a biased estimator of θ and compute the bias. b Find a function of Y that is an unbiased estimator of θ.

Answer 1

Explanation:

The complete question is

The reading on a voltage meter connected to a test circuit is uniformly distributed over the interval (θ, θ + 1), where θ is the true but unknown voltage of the circuit. Suppose that Y1,Y2,...,Yn denotearandomsampleofsuchreadings.Let Y be the sample mean. a) Show that Y is a biased estimator of θ and compute the bias. b Find a function of Y that is an unbiased estimator of θ.

Recall that an unbiased estimator Y of a parameter
`\theta` is a function of a random sample for which we have that

`E[Y] = \theta`. When this is not the case, the quantity
`E[Y]-\theta` is called the biased of the estimator.

Recall that for each i,
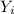`Y_i` is uniformly distributed on the interval
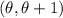`(\theta,\theta+1)`, then
`E[Y_i] = (\theta + \theta +1 )/(2) = \theta + (1)/(2)`.

Then, using the linear property of the expeted value, we have that

`E[Y] = E[(1)/(n)\sum_(i=1)^(n) Y_i] = (1)/(n)\sum_(i=1)^(n) E[Y_i] = (n (\theta+0.5))/(n) = \theta + 0.5`

So, Y is a biased estimator of [tex]\theta [/tex} and the bias is 0.5.

b) We can easily obtain an unbiased estimator of theta by simply substracting the bias to the biased estimator, that is Y-0.5 is an unbiased estimator of the parameter theta.