Answer:
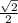
Explanation:
First, we see that we have the term
 . When we have a negative exponent, we can always flip the number to its reciprocal and take the reciprocal to the positive exponent.
. When we have a negative exponent, we can always flip the number to its reciprocal and take the reciprocal to the positive exponent.
For example: here we have
 . To turn this into positive exponents, we now have:
. To turn this into positive exponents, we now have:
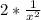 .
.
So, we have:
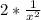 = 4
= 4
Divide both sides by 4 and multiply both sides by x^2:
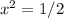
Square root both sides:
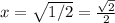
Thus, the answer is
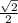 .
.
Hope this helps!