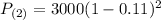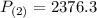Question

The florida manatee population is 3,000 and is decreasing by 11% each year. Write a function for this situation.

Answer 1

Answer:
`P_((t))=P_(o)(1-0.11)^(t)`

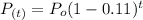
Explanation:

According to the described situation, the current manatee population is 3000, if it decreases
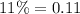`11\%=0.11` each year this means in one year the manatee population will be:

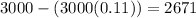`3000-(3000(0.11))=2671` (1)

And the next year:

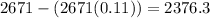`2671-(2671(0.11))=2376.3` (2)

This mean each year the population will be
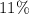`11\%` less than last year.

So, in this case we can use the following function to express this decrease:

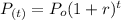`P_((t))=P_(o)(1+r)^(t)` (3)

Where:

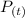`P_((t))` Is the number of manaties at time
`t`

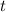
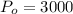`P_(o)=3000` is the current number of manaties (this year)

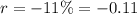`r=-11\%=-0.11` is the decrease rate of the population

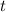`t` is the time (in years)

For example, if we want to estimate the number of manaties for next year,
`t=1`:

`P_((1))=3000(1-0.11)^(1)`

`P_((1))=2670`

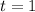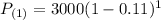
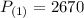
If we want to estimate the number of manaties in two yeas,
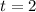`t=2`:

`P_((2))=3000(1-0.11)^(2)`

`P_((2))=2376.3`

Answer 2

`P=3000(0.89)^t`

Explanation:

It was given that, florida manatee population is 3,000 and is decreasing by 11% each year.

We want to write a function for this situation.

Since the population is decreasing annually, it is modelled by:

`P=P_0(1-r\%)^t`

We substitute the give initial population and rate of decrease to get:

`P=3000(1-0.11)^t`

This simplifies to:

`P=3000(0.89)^t`