Answer:
Part B)
97.5%
Part C)
81.5%
Explanation:
Part B)
ACT math scores for a particular year are approximately normally distributed
with a mean of 28 and a standard deviation of 2.4.
We want to find the Probability that a randomly selected score is less than 32.8.
First, we determine the z-score of 32.8 using:
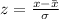

According to the Empirial rule, 95% of the distribution under the normal distribution curve is within 2 standard deviations of the mean, (-2 to 2).
This means from (0 to 2) corresponds to 47.5%.
Therefore the area less than 2, will be equal to:
50%+47.5%=97.5%
Part C)
We want to find the Probability that a randomly selected score is between 25.6 and 32.8.
That is

We convert to z-scores to get:

This means that;
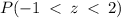
Using the empirical rule again, 68% is within (-1 to 1), therefore 34% is within (-1 to 0).
And we know (-1 to 2)=(-1 to 0)+(0,2).
Therefore we have 34% +47.5%=81.5%
The required probability is 81.5%