Given:
Right triangle with one angle 45°
To find:
The value of q and r.
Solution:
Opposite to θ = 16
Adjacent to θ = r
Hypotenuse = q
Using trigonometric ratio formula:
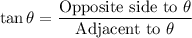
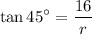
The value of tan 45° = 1
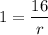
Do cross multiplication, we get
r = 16
Using trigonometric ratio formula:
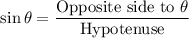
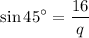
The value of sin 45° =
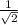 .
.
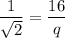
Do cross multiplication, we get
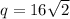
The value of r is 16 and the value of q is
 .
.