Question

The value of an investment of $1000 earning 7% compounded annually is V(I, R) = 1000 1 + 0.07(1 − R) 1 + I 10 where I is the annual rate of inflation and R is the tax rate for the person making the investment. Calculate VI(0.03, 0.28) and VR(0.03, 0.28). (Round your answers to two decimal places.) VI(0.03, 0.28) = VR(0.03, 0.28) =

Answer 1

`V_(I)=-11812.39`

`V_(R)=-810.81`

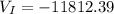
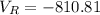
Step-by-step explanation:

We will first state the equation.

`V(I,R)=1000[(1+0.07(1-R))/(1+I)]^(10)`

Where:

I = annual rate of inflation;

R = the tax rate for the person making the investment.

We first determine the partial derivatives with respect to I and R.

`(dV)/(dI)=-10000((1+0.07(1-R))^(10))/((1+I)^(11))`

`(dV)/(dR)=-700((1+0.07(1-R))^(9))/((1+I)^(10))`

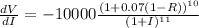
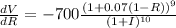
VI(0.03, 0.28)

`(dV(0.03,0.28)/(dI)=-10000((1+0.07(1-0.28))^(10))/((1+0.03)^(11))`

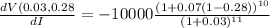
=-11812.39

`(dV(0.03,0.28))/(dR)=-700((1+0.07(1-0.28))^(9))/((1+0.03)^(10))`

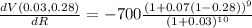
=-810.81