Question

Determine whether a tangent line to circle O is shown in the diagram, for AB = 7, OB = 3.75, and AO = 8. Explain your reasoning. (The figure is not drawn to scale.)

Answer 1

The line AB is not tangent to circle O

Explanation:

we know that

If AB is tangent to circle O at point B

then

AB is perpendicular to OB (radius) and ABO is a right triangle

Verify

Applying the Pythagorean Theorem

`AO^2=AB^2+OB^2`

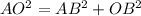
substitute the given values

`8^2=7^2+3.75^2`

`64=49+14.0625`

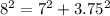
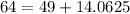
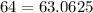`64=63.0625` -----> is not true

so

The triangle not satisfy the Pythagorean Theorem

therefore

The line AB is not tangent to circle O