Answer:
-5 and 4
Explanation:
Use a system of equations. Let
 be the first number and
be the first number and
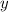 be the second number
be the second number
The first equation will be a product,
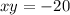 , and the second will be a sum,
, and the second will be a sum,
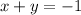
Solve the second equation for
 , which results in
, which results in
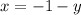 , and substitute into the first equation.
, and substitute into the first equation.
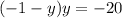
Distribute
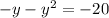
Set equal to zero
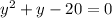
Factor
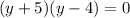
So
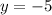 or
or
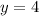
When
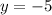 , then
, then
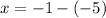 or
or
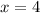
When
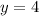 , then
, then
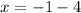 or
or
