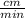Answer:
The center velocity of both gears is same & equal to 2034.72
Explanation:
Given data
 = 5 cm
= 5 cm
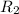 = 3 cm
= 3 cm
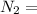 36 rev in 20 sec
36 rev in 20 sec
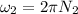
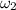 = 2 × 3.14 × 1.8
= 2 × 3.14 × 1.8
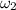 = 11.304
= 11.304
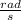
We know that for the set of gears
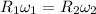
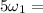 3 × 11.304
3 × 11.304
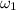 = 6.7824
= 6.7824
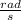
liner velocity of the first gear
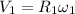
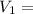 5 × 6.7824
5 × 6.7824
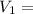 33.912
33.912
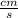
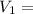 20.34.72
20.34.72
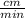
liner velocity of the second gear
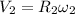
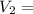 3 × 11.304
3 × 11.304
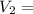 2034.72
2034.72
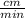
Therefore the center velocity of both gears is same & equal to 2034.72